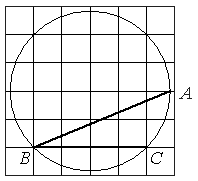
Найдите угол ABC. Ответ дайте в градусах.
Угол ABC (обозначим его α) является
вписанным в окружность, следовательно, он равен половине центрального угла, опирающегося на ту же дугу 2α (по
теореме).
Найдем
центральный угол через тангенс. Рассмотрим
центральный ("синий") угол и проведенный в нем катет ("зеленый").
tg(2α)=2/2=1
По
таблице угол 2α=45°
α=45°/2=22,5°
Ответ: 22,5
Поделитесь решением
Присоединяйтесь к нам...
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
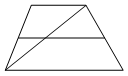Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
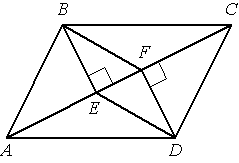В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
Основания равнобедренной трапеции равны 3 и 17, боковая сторона равна 25. Найдите длину диагонали трапеции.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: