В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=16.
∠QNM - является
вписанным в окружность и опирается на дугу QM.
∠QPM тоже является
вписанным в окружность и опирается на дугу QM.
Следовательно, эти углы равны.
∠QNM=∠QPM
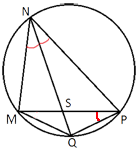Рассмотрим треугольники NPQ и SPQ.
∠SQP - общий
∠QNP=∠SPQ
По
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, NQ/QP=QP/SQ
NQ=QP2/SQ=442/16=121
NS=NQ-SQ=121-16=105
Ответ: NS=105
Поделитесь решением
Присоединяйтесь к нам...
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
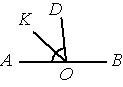Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-04-11 21:10:09) Администратор: Равенство NQ/QP=QP/SQ домножаем на QP, получаем NQ=QP*QP/SQ=QP2/SQ
(2015-04-11 21:05:29) Администратор: Задачи с 2014 года, но они актуальны и на 2015 год.
(2015-04-11 19:30:49) : NQ=QP2/SQ=442/16=121почему здесь квадрат?
(2015-04-11 19:30:48) : NQ=QP2/SQ=442/16=121почему здесь квадрат?
(2015-04-11 19:23:51) : а здесь задачи с какого года ?
(2015-04-11 19:23:48) : а здесь задачи с какого года ?
(2015-02-23 07:24:33) Александр: Кратко и доступно