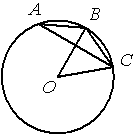
Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=50°, этот угол является
центральным, соответственно дуга ВC тоже равна 50°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 50/2=25.
Ответ: /BAC=25°.
Поделитесь решением
Присоединяйтесь к нам...
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Площадь прямоугольного треугольника равна 8√
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
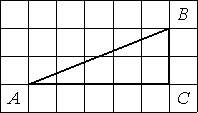Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: