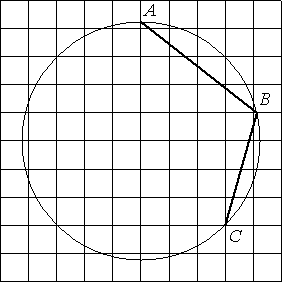
Найдите угол ABC. Ответ дайте в градусах.
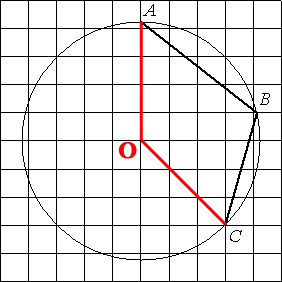Проведем два отрезка от центра окружности к точкам А и С, как показано на рисунке.
По координатной сетке видно, что получившийся угол AOC равен 135° (прямой угол + половина от прямого угла, 90°+45°=135°).
∠AOC является
центральным для окружности, следовательно градусная мера дуги, на которую он опирается (ABC), тоже равна 135°.
Следовательно, бОльшая дуга имеет градусную меру 360°-135°=225°
∠ABC -
вписанный угол, опирается на бОльшую дугу и по
теореме равен 225°/2=112,5°
Ответ: 112,5
Поделитесь решением
Присоединяйтесь к нам...
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMB.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
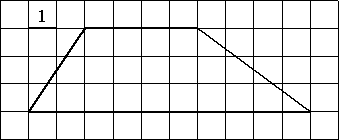Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: