Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Вариант №1
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=∠A+66°+84°
∠A=180°-66°-84°=30°
По
теореме синусов:
2R=BC/sin∠A
2R=BC/sin30°=BC/(1/2)=2BC
R=BC=15
Ответ: 15
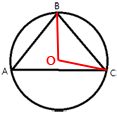Проведем два отрезка из центра к точкам B и C, как показано на рисунке.Поделитесь решением
Присоединяйтесь к нам...
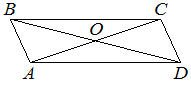Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
В треугольнике ABC угол C равен 90°, AC=6, tgA=2√
Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
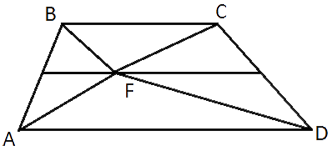На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: