ОГЭ, Математика.
Геометрия: Задача №C4C0EC

Задача №627 из 1087
Условие задачи:

Диагональ прямоугольника образует угол 75° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение задачи:

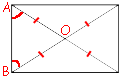Диагонали прямоугольника равны и точкой пересечения делятся пополам (по свойству прямоугольника).
Рассмотрим треугольник ABO (см. рисунок).
AO=BO (как мы только что выяснили).
Следовательно, треугольник ABO - равнобедренный.
По первому свойству равнобедренного треугольника:
∠OBA=∠OAB
По теореме о сумме углов треугольника:
180°=∠AOB+∠OBA+∠OAB
180°=∠AOB+75°+75°
∠AOB=30°
Ответ: 30

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №08CAB1

Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Средняя линия трапеции равна сумме её оснований.
3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.