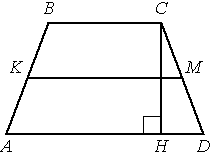
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
Средняя линия трапеции Lср=(AD+BC)/2, отсюда AD=2*Lср-BC.
Проведем еще одну высоту из вершины B
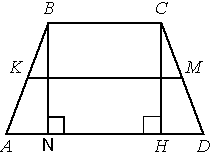и рассмотрим треугольники CDH и ABN. AB=CD (по условию задачи), BN=CH, т.к. BCHN -
прямоугольник, образованный параллельными сторонами трапеции и перпендикулярами к ним. Следовательно, применив
теорему Пифагора, получим, что HD=NA
AD=AN+NH+HD, AD=2*HD+NH, NH=BC (т.к. BCHN - прямоугольник), тогда AD=2*HD+BC,
HD=(AD-BC)/2
Ранее мы выяснили, что AD=2*Lср-BC=2*16-4=28, тогда HD=(28-4)/2=12.
Ответ: HD=12.
Поделитесь решением
Присоединяйтесь к нам...
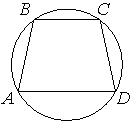Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7.5, а AB=2.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: