
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ412 –Η–Ζ 1087 |
 –Γ―²–Ψ―Ä–Ψ–Ϋ–Α AB –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD –≤–¥–≤–Ψ–Β –±–Ψ–Μ―¨―à–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AD. –Δ–Ψ―΅–Κ–Α K βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ DK βÄî –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―É–≥–Μ–Α ADC.
–Γ―²–Ψ―Ä–Ψ–Ϋ–Α AB –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD –≤–¥–≤–Ψ–Β –±–Ψ–Μ―¨―à–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AD. –Δ–Ψ―΅–Κ–Α K βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ DK βÄî –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―É–≥–Μ–Α ADC.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ AKD.
AK=AD (–Ω–Ψ ―É―¹–Μ–Ψ–≤–Η―é –Ζ–Α–¥–Α―΅–Η), ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ
―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―΄–Ι.
–ü–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ∠ADK=∠AKD
∠AKD=∠KDC (―².–Κ. ―ç―²–Ψ
–Ϋ–Α–Κ―Ä–Β―¹―²-–Μ–Β–Ε–Α―â–Η–Β ―É–≥–Μ―΄).
–ü–Ψ–Μ―É―΅–Α–Β―²―¹―è, ―΅―²–Ψ ∠ADK=∠AKD=∠KDC.
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ DK -
–±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –€–Β–¥–Η–Α–Ϋ–Α BM –Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α AP ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β K, –¥–Μ–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AC –≤―²―Ä–Ψ–Β –±–Ψ–Μ―¨―à–Β –¥–Μ–Η–Ϋ―΄ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α AKM –Κ –Ω–Μ–Ψ―â–Α–¥–Η ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α KPCM.
–€–Β–¥–Η–Α–Ϋ–Α BM –Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α AP ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β K, –¥–Μ–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AC –≤―²―Ä–Ψ–Β –±–Ψ–Μ―¨―à–Β –¥–Μ–Η–Ϋ―΄ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α AKM –Κ –Ω–Μ–Ψ―â–Α–¥–Η ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α KPCM.
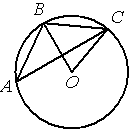 –Δ–Ψ―΅–Κ–Α –û βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, /BAC=20¬Α (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BOC (–≤ –≥―Ä–Α–¥―É―¹–Α―Ö).
–Δ–Ψ―΅–Κ–Α –û βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, /BAC=20¬Α (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BOC (–≤ –≥―Ä–Α–¥―É―¹–Α―Ö).
–€–Β–¥–Η–Α–Ϋ–Α BM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―è–≤–Μ―è–Β―²―¹―è –¥–Η–Α–Φ–Β―²―Ä–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―â–Β–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ―É BC –≤ –Β―ë ―¹–Β―Ä–Β–¥–Η–Ϋ–Β. –ù–Α–Ι–¥–Η―²–Β ―ç―²–Ψ―² –¥–Η–Α–Φ–Β―²―Ä, –Β―¹–Μ–Η –¥–Η–Α–Φ–Β―²―Ä –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―Ä–Α–≤–Β–Ϋ 8.
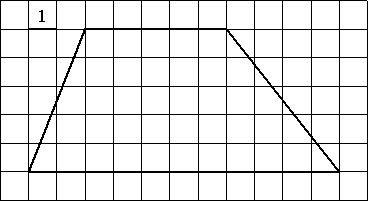 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–Ι –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–Ι –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–≥–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–≥–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.

–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2014-05-26 22:01:15) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –ï–Μ–Β–Ϋ–Α, –Ω–Ψ―²–Ψ–Φ―É, ―΅―²–Ψ ∠ADK=∠AKD, –Α ∠AKD=∠KDC.
(2014-05-26 18:30:51) –ï–Μ–Β–Ϋ–Α: –Ω–Ψ―΅–Β–Φ―É ∠ADK=∠KDC.