Укажите номера верных утверждений.
1) Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая медиана равнобедренного треугольника является его биссектрисой.
Рассмотрим каждое утверждение:
1) "Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны", это утверждение верно, т.к. это один из
признаков подобия.
2) "Сумма смежных углов равна 180°", это утверждение верно (по
определению).
3) "Любая медиана равнобедренного треугольника является его биссектрисой", это утверждение неверно, т.к. по
свойству равнобедренного треугольника, только
медиана, проведенная к основанию, является и
биссектрисой, и
высотой.
Поделитесь решением
Присоединяйтесь к нам...
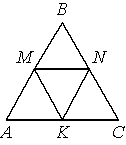В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
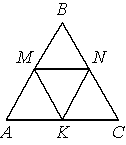В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
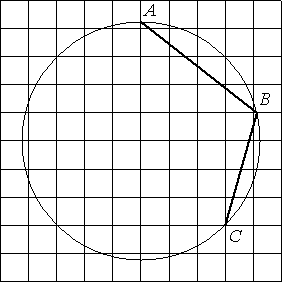Найдите угол ABC. Ответ дайте в градусах.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-02-09 22:51:17) Администратор: Оксана, если в треугольниках равны все 3 угла, то два угла этих треугольников, тем более равны, поэтому эту утверждение верно.
(2019-02-09 12:55:32) Оксана: 1 утверждение неверно, так как первый признак подобия гласит, что треугольники могут быть подобны по 2ум равным углам. Все остальные вариации этого утверждения не являются верными.
(2014-04-30 16:44:21) Администратор: Вика, по первому признаку подобия, в ответе есть ссылка.
(2014-04-30 16:42:36) Вика: а почему 1 утверждение верно?