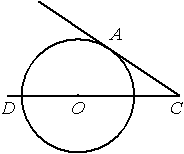
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
110°.
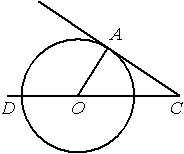Проведем отрезок ОА.
/DOA -
центральный угол для данной окружности. Он опирается на дугу AD, равную 110°. Следовательно, /DOA тоже равен 110°.
/AOC -
смежный углу DOA, поэтому /AOC=180°- /DOA=180°-110°=70°.
Треугольник ACO -
прямоугольный, т.к. радиус всегда перпендикулярен
касательной (по
свойству касательной). Т.е. /ОАС=90°. Применяя
теорему о сумме углов треугольника, можем записать:
180°=/AСO+/CAO+/AOC.
/AСO=180°-/CAO-/AOC=180°-90°-70°=20°.
Ответ: /ACO=20°.
Поделитесь решением
Присоединяйтесь к нам...
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=177°. Найдите величину угла BOC. Ответ дайте в градусах.
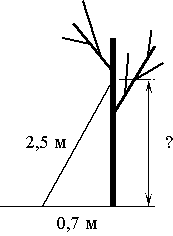Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: