В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 67. Найдите площадь четырёхугольника ABMN.
Вариант №1
MN -
средняя линия треугольника ABC, по теореме о средней линии NM=AB/2 => 2NM=AB.
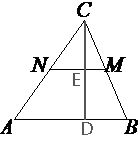Проведем
высоту из вершины С.
SCNM=1/2*CE*NM=67 (по условию).
CE*NM=134
Рассмотрим треугольник ACD, NE||AD и идет из середины стороны AC, следовательно NE -
средняя линия для треугольника ACD, значит CE=ED.
ABMN - трапеция (по
определению), тогда
SABMN=(NM+AB)/2*ED. Подставляем ранее выявленные равенства, получаем:
SABMN=(NM+2NM)/2*CE=3NM/2*CE=1,5NM*CE=1,5*134=201
Ответ: 201
MN -
средняя линия треугольника ABC, по теореме о средней линии MN=AF=FB.Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
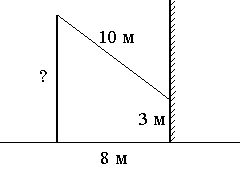От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7.5, а AB=2.
Стороны AC, AB, BC треугольника ABC равны 2√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: