
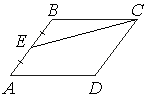
 Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
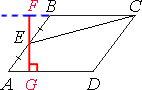 Проведем перпендикулярный отрезок от одной стороны
параллелограмма к другой через точку Е, как показано на рисунке.
Проведем перпендикулярный отрезок от одной стороны
параллелограмма к другой через точку Е, как показано на рисунке.
Обозначим концы отрезка как F и G.
FG - высота параллелограмма, так как перпендикулярен двум сторонам (мы сами так его провели).
Площадь параллелограмма:
SABCD=FG*AD=FG*BC
Рассмотрим треугольники AEG и BEF:
AE=EB (по условию задачи).
∠AEG=∠BEF (они вертикальные).
∠GAE=∠FBE (они накрест-лежащие).
Тогда, по второму признаку равенства треугольников, данные треугольники равны.
Это означает, что EF=EG=FG/2
EF - высота треугольника CBE.
Воспользуемся формулой
площади треугольника через высоту и основание:
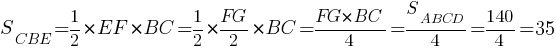
Ответ: 35
Поделитесь решением
Присоединяйтесь к нам...
 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
 Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
 В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
 В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.



Комментарии:
(2022-10-06 01:54:59) : в треугольнике авс с равен 114 сторонв ас и вс равны найдите угол в. ответ дайте в градусах