Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Средняя линия трапеции равна сумме её оснований.
3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Рассмотрим каждое утверждение.
1) "Площадь треугольника меньше произведения двух его сторон". Площадь треугольника можно вычислить по формуле Sтреугольника=1/2*a*b*sinC, где С - угол между сторонами a и b. Т.к. значение синуса не может быть больше единицы, получается, что a*b всегда больше 1/2*a*b*sinC. Поэтому это утверждение верно.
2) "Средняя линия трапеции равна сумме её оснований" - это утверждение неверно, так как средняя линия равна полусумме оснований (по
определению).
3) "Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны". Это утверждение верно по
признаку подобия.
Ответ: 1) и 3)
Поделитесь решением
Присоединяйтесь к нам...
ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов остроугольного треугольника равна 180°.
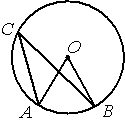Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
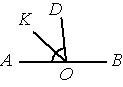Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 12°?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: