
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ556 –Η–Ζ 1087 |
 –£ –≤―΄–Ω―É–Κ–Μ–Ψ–Φ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β NPQM –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ NQ ―è–≤–Μ―è–Β―²―¹―è –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι ―É–≥–Μ–Α PNM –Η –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―²―¹―è ―¹ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨―é PM –≤ ―²–Ψ―΅–Κ–Β S. –ù–Α–Ι–¥–Η―²–Β NS, –Β―¹–Μ–Η –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ –Ψ–Κ–Ψ–Μ–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α NPQM –Φ–Ψ–Ε–Ϋ–Ψ –Ψ–Ω–Η―¹–Α―²―¨ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, PQ=44, SQ=16.
–£ –≤―΄–Ω―É–Κ–Μ–Ψ–Φ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β NPQM –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ NQ ―è–≤–Μ―è–Β―²―¹―è –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι ―É–≥–Μ–Α PNM –Η –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―²―¹―è ―¹ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨―é PM –≤ ―²–Ψ―΅–Κ–Β S. –ù–Α–Ι–¥–Η―²–Β NS, –Β―¹–Μ–Η –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ –Ψ–Κ–Ψ–Μ–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α NPQM –Φ–Ψ–Ε–Ϋ–Ψ –Ψ–Ω–Η―¹–Α―²―¨ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, PQ=44, SQ=16.
∠QNM - ―è–≤–Μ―è–Β―²―¹―è
–≤–Ω–Η―¹–Α–Ϋ–Ϋ―΄–Φ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ –Η –Ψ–Ω–Η―Ä–Α–Β―²―¹―è –Ϋ–Α –¥―É–≥―É QM.
∠QPM ―²–Ψ–Ε–Β ―è–≤–Μ―è–Β―²―¹―è
–≤–Ω–Η―¹–Α–Ϋ–Ϋ―΄–Φ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ –Η –Ψ–Ω–Η―Ä–Α–Β―²―¹―è –Ϋ–Α –¥―É–≥―É QM.
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―ç―²–Η ―É–≥–Μ―΄ ―Ä–Α–≤–Ϋ―΄.
∠QNM=∠QPM
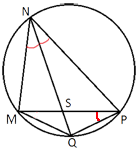 –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η NPQ –Η SPQ.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η NPQ –Η SPQ.
∠SQP - –Ψ–±―â–Η–Ι
∠QNP=∠SPQ
–ü–Ψ
–Ω–Β―Ä–≤–Ψ–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É –Ω–Ψ–¥–Ψ–±–Η―è ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤, –¥–Α–Ϋ–Ϋ―΄–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η
–Ω–Ψ–¥–Ψ–±–Ϋ―΄.
–Δ–Ψ–≥–¥–Α, NQ/QP=QP/SQ
NQ=QP2/SQ=442/16=121
NS=NQ-SQ=121-16=105
–û―²–≤–Β―²: NS=105
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –£ –≤―΄–Ω―É–Κ–Μ–Ψ–Φ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β NPQM –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ NQ ―è–≤–Μ―è–Β―²―¹―è –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι ―É–≥–Μ–Α PNM –Η –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―²―¹―è ―¹ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨―é PM –≤ ―²–Ψ―΅–Κ–Β S. –ù–Α–Ι–¥–Η―²–Β NS, –Β―¹–Μ–Η –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ –Ψ–Κ–Ψ–Μ–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α NPQM –Φ–Ψ–Ε–Ϋ–Ψ –Ψ–Ω–Η―¹–Α―²―¨ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, PQ=86, SQ=43.
–£ –≤―΄–Ω―É–Κ–Μ–Ψ–Φ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β NPQM –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ NQ ―è–≤–Μ―è–Β―²―¹―è –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι ―É–≥–Μ–Α PNM –Η –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―²―¹―è ―¹ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨―é PM –≤ ―²–Ψ―΅–Κ–Β S. –ù–Α–Ι–¥–Η―²–Β NS, –Β―¹–Μ–Η –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ –Ψ–Κ–Ψ–Μ–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α NPQM –Φ–Ψ–Ε–Ϋ–Ψ –Ψ–Ω–Η―¹–Α―²―¨ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, PQ=86, SQ=43.
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ ∠BAC=64¬Α, AD βÄî –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ BAD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ ∠BAC=64¬Α, AD βÄî –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ BAD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Α―è –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC, –Κ–Α―¹–Α–Β―²―¹―è –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ –≤ ―²–Ψ―΅–Κ–Α―Ö M, K –Η P. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Μ―΄ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Β―¹–Μ–Η ―É–≥–Μ―΄ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α MKP ―Ä–Α–≤–Ϋ―΄ 38¬Α, 78¬Α –Η 64¬Α.
–û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Α―è –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC, –Κ–Α―¹–Α–Β―²―¹―è –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ –≤ ―²–Ψ―΅–Κ–Α―Ö M, K –Η P. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Μ―΄ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Β―¹–Μ–Η ―É–≥–Μ―΄ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α MKP ―Ä–Α–≤–Ϋ―΄ 38¬Α, 78¬Α –Η 64¬Α.
 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–Ι –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–Ι –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
 –£ ―²―Ä–Α–Ω–Β―Ü–Η―é, ―¹―É–Φ–Φ–Α –¥–Μ–Η–Ϋ –±–Ψ–Κ–Ψ–≤―΄―Ö ―¹―²–Ψ―Ä–Ψ–Ϋ –Κ–Ψ―²–Ψ―Ä–Ψ–Ι ―Ä–Α–≤–Ϋ–Α 24, –≤–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―¹―Ä–Β–¥–Ϋ–Β–Ι –Μ–Η–Ϋ–Η–Η ―²―Ä–Α–Ω–Β―Ü–Η–Η.
–£ ―²―Ä–Α–Ω–Β―Ü–Η―é, ―¹―É–Φ–Φ–Α –¥–Μ–Η–Ϋ –±–Ψ–Κ–Ψ–≤―΄―Ö ―¹―²–Ψ―Ä–Ψ–Ϋ –Κ–Ψ―²–Ψ―Ä–Ψ–Ι ―Ä–Α–≤–Ϋ–Α 24, –≤–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―¹―Ä–Β–¥–Ϋ–Β–Ι –Μ–Η–Ϋ–Η–Η ―²―Ä–Α–Ω–Β―Ü–Η–Η.


–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2015-04-11 21:10:09) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –†–Α–≤–Β–Ϋ―¹―²–≤–Ψ NQ/QP=QP/SQ –¥–Ψ–Φ–Ϋ–Ψ–Ε–Α–Β–Φ –Ϋ–Α QP, –Ω–Ψ–Μ―É―΅–Α–Β–Φ NQ=QP*QP/SQ=QP2/SQ
(2015-04-11 21:05:29) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –½–Α–¥–Α―΅–Η ―¹ 2014 –≥–Ψ–¥–Α, –Ϋ–Ψ –Ψ–Ϋ–Η –Α–Κ―²―É–Α–Μ―¨–Ϋ―΄ –Η –Ϋ–Α 2015 –≥–Ψ–¥.
(2015-04-11 19:30:49) : NQ=QP2/SQ=442/16=121–Ω–Ψ―΅–Β–Φ―É –Ζ–¥–Β―¹―¨ –Κ–≤–Α–¥―Ä–Α―²?
(2015-04-11 19:30:48) : NQ=QP2/SQ=442/16=121–Ω–Ψ―΅–Β–Φ―É –Ζ–¥–Β―¹―¨ –Κ–≤–Α–¥―Ä–Α―²?
(2015-04-11 19:23:51) : –Α –Ζ–¥–Β―¹―¨ –Ζ–Α–¥–Α―΅–Η ―¹ –Κ–Α–Κ–Ψ–≥–Ψ –≥–Ψ–¥–Α ?
(2015-04-11 19:23:48) : –Α –Ζ–¥–Β―¹―¨ –Ζ–Α–¥–Α―΅–Η ―¹ –Κ–Α–Κ–Ψ–≥–Ψ –≥–Ψ–¥–Α ?
(2015-02-23 07:24:33) –ê–Μ–Β–Κ―¹–Α–Ϋ–¥―Ä: –ö―Ä–Α―²–Κ–Ψ –Η –¥–Ψ―¹―²―É–Ω–Ϋ–Ψ