
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
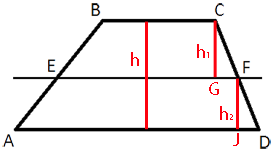 Проведем
высоты h1 и h2 как показано на рисунке.
Проведем
высоты h1 и h2 как показано на рисунке.
Рассмотрим треугольники CFG и FDJ.
∠CGF=∠FJD=90° (т.к. мы проводили
высоты).
∠CFG=∠FDJ (т.к. это
соответственные углы).
Следовательно, эти треугольники
подобны по
первому признаку подобия.
По
определению подобных треугольников:
CF/DF=CG/FJ=4/3
Для простоты обозначим:
CG=h1
FJ=h2
SEBCF=(CB+EF)*h1/2
SAEFD=(EF+AD)*h2/2
SABCD=(BC+AD)*(h1+h2)/2
Так сумма площадей этих
трапеций равна площади большой трапеции, то запишем:
(CB+EF)*h1/2+(EF+AD)*h2/2=(BC+AD)*(h1+h2)/2
(CB+EF)*h1+(EF+AD)*h2=(BC+AD)*(h1+h2)
CB*h1+EF*h1+EF*h2+AD*h2=BC*h1+BC*h2+AD*h1+AD*h2
CB*h1+EF*h1-BC*h1-AD*h1=BC*h2+AD*h2-EF*h2-AD*h2
(CB+EF-BC-AD)*h1=(BC+AD-EF-AD)*h2
(EF-AD)*h1=(BC-EF)*h2
h1/h2=(BC-EF)/(EF-AD)
4/3=(14-EF)/(EF-42)
4(EF-42)=3(14-EF)
4*EF-168=42-3*EF
7*EF=210
EF=30
Ответ: EF=30
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
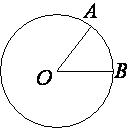 На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
 Площадь прямоугольного треугольника равна 2√
Площадь прямоугольного треугольника равна 2√


Комментарии:
(2017-03-06 23:30:43) Администратор: Алина, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-03-06 11:04:23) АЛИНА: на прямой последовательно отмечены точки L,K,P,F,E,так что LK=KP=PF=FE=2см.Какие ещё равные отрезки определяются по этим точкам?Записать эти отрезки и найти их длины
(2016-12-18 20:10:06) Администратор: Вероника, аналогично этой.
(2016-12-18 18:45:22) Вероника: № 4) Прямая, параллельная основаниям трапеции АВСD, пересекает её боковые стороны АВ и СD в точках Е и F соответственно. Найдите длину отрезка ЕF, если АD = 45, ВС = 20, СF : DF = 4 : 1. Как решить эту задачу ?
(2015-05-10 19:03:07) Администратор: Мария, я дописал в решение пару строк, чтобы стало понятней.
(2015-05-10 16:28:56) Мария: Помогите пожалуйста, как из (CB+EF)*h1+(EF+AD)*h2=(BC+AD)*(h1+h2) получилось (CB+EF-BC-AD)*h1=(BC+AD-EF-AD)*h2 ?
(2015-05-09 14:45:52) Администратор: Елена, отличный вариант, скоро его опубликую, спасибо!
(2015-05-08 21:51:36) Елена: Проведём из вершины С прямую параллельную АВ. Она разобьёт АD на отрезки, равные 14 и 28 , а EF на отрезки 14 и х. Трапеция будет разделена на параллелограмм и треугольник. Прямая EF делит этот треугольник на два подобных треугольника. Коэффициент подобия 4/7. х=16, тогда EF=14+16=30