
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
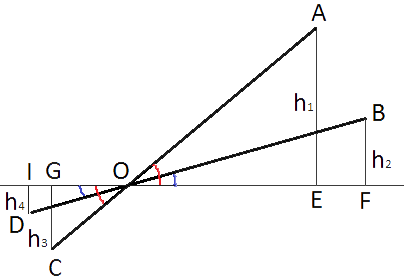 Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников.
Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников.
h1 - изначальная высота длинного плеча журавля.
h2 - конечная высота длинного плеча журавля.
h3 - изначальная высота короткого плеча журавля.
h4 - конечная высота короткого плеча журавля.
h3-h4=1,5 метра (по условию задачи).
Нам надо найти:
h1-h2=?.
Рассмотрим треугольники AOE и COG.
1) ∠AOE=∠COG, т.к. они
вертикальные.
2) ∠AEO=∠CGO=90°
Следовательно, треугольники AOE и COG
подобны (по первому признаку подобия). Отсюда следует, что h1/OA=h3/OC.
Треугольники BOF и DOI тоже
подобны (аналогично предыдущим треугольникам).
Тогда:
h2/OB=h4/OD
OA=OB и OC=OD (так как длины плеч журавля не меняются), тогда:
h2/OA=h4/OC
Вычтем из первого равенства второе:
h1/OA-h2/OA=h3/OC-h4/OC.
(h1-h2)/OA=(h3-h4)/OC.
(h1-h2)/6=1,5/2.
h1-h2=6*1,5/2=4,5.
Ответ: 4,5.
Поделитесь решением
Присоединяйтесь к нам...
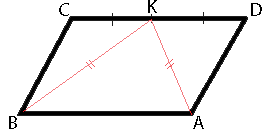 В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
 В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.
 Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
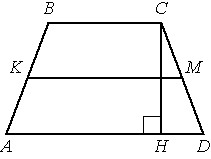 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.


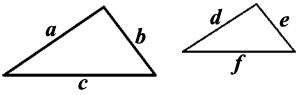
Комментарии: