Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
ABCD -
трапеция, следовательно, AD||BC.
∠CBD=∠ADB (т.к. это
накрест-лежащие углы для параллельных прямых AD и BC).
Рассмотрим отношения сторон:
BC/BD=5/10=1/2
BD/AD=10/20=1/2
Тогда по
второму признаку подобия треугольников, треугольники CBD и BDA подобны.
Поделитесь решением
Присоединяйтесь к нам...
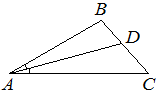В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
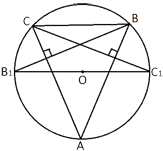Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
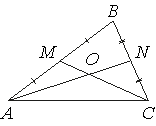Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: