Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
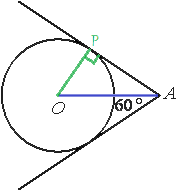Проведем отрезок АО.
Обозначим одну из точек касания окружности и касательной как Р.
Проведем отрезок ОР.
ОР является радиусом и перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР. Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР. АО является биссектрисой угла, образованного касательными (свойство касательных прямых).
Следовательно, угол РАО равен половине данного угла, т.е. 30°.
sin∠PAO=sin∠30°=1/2 (табличное значение).
Так же sin∠PAO=ОР/АО (по определению синуса).
sin∠30°=1/2=ОР/АО
AO=2*ОР=2*8=16.
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
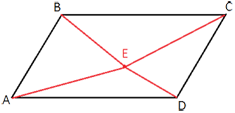Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: