Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
AB=BC=CD=AD=DH+CH=8+2=10 (по
определению ромба).
Рассмотрим треугольник AHD.
AHD -
прямоугольный (т.к. AH -
высота), тогда по
теореме Пифагора: AD2=AH2+DH2
102=AH2+82
100=AH2+64
AH2=36
AH=6
Ответ: 6
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
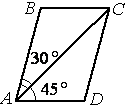Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: