Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
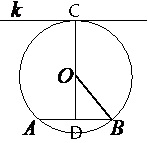Проведем отрезок OB как показано на рисунке.
Расстояние от
хорды AB до параллельной ей
касательной k обозначено как CD.
CD=OC+OD, OC - это радиус окружности, найдем OD.
По условию задачи k||AB. CD перпендикулярен k (по
свойству касательной), тогда CD перпендикулярен и AB (т.к. CD - секущая для параллельных прямых, и внутренние
накрест-лежащие углы равны), значит треугольник OBD
прямоугольный.
DB=AB/2=96/2=48 (по
второму свойству хорды)
OB равен радиусу окружности.
Тогда по
теореме Пифагора:
OB2=OD2+DB2
502=OD2+482
2500=OD2+2304
OD2=2500-2304=196
OD=14
CD=OC+OD=50+14=64
Ответ: 64
Поделитесь решением
Присоединяйтесь к нам...
Середина M стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 129° и 96°.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
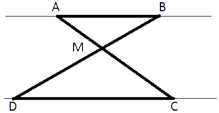Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
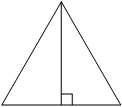Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
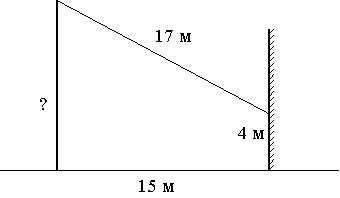От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: