Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 5,25, а AB=9.
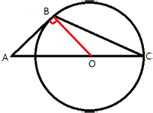Отрезок AC равен сумме отрезков AO и OC, OC - равен радиусу окружности, т.е. 5,25/2=2,625. Найдем AO.
Проведем отрезок BO. BO - так же является радиусом окружности. AB -
касательная к окружности, следовательно AB перпендикулярен BO (по
свойству касательной).
Значит треугольник ABO -
прямоугольный, тогда по
теореме Пифагора:
AO2=AB2+BO2
AO2=92+2,6252
AO2=81+6,890625=87,890625
AO=9,375
AC=AO+OC=9,375+2,625=12
Ответ: AC=12
Поделитесь решением
Присоединяйтесь к нам...
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=36, BC=42 и CD=24.
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
В треугольнике ABC угол C прямой, AC=6, cosA=0,6. Найдите AB.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?
Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: