
 Катеты прямоугольного треугольника равны 2√
Катеты прямоугольного треугольника равны 2√
 Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=12+(2√
AB2=1+4*6=25
AB=5
Меньший угол лежит напротив меньшей стороны, 1<2√
Ответ: 0,2
Поделитесь решением
Присоединяйтесь к нам...
 Сторона ромба равна 28, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 28, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
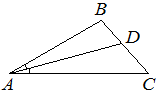 В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.

Комментарии: