
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ523 –Η–Ζ 1087 |
 –£―΄―¹–Ψ―²–Α BH ―Ä–Ψ–Φ–±–Α ABCD –¥–Β–Μ–Η―² –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ―É AD –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η AH=21 –Η HD=54. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Ψ–Φ–±–Α.
–£―΄―¹–Ψ―²–Α BH ―Ä–Ψ–Φ–±–Α ABCD –¥–Β–Μ–Η―² –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ―É AD –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η AH=21 –Η HD=54. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Ψ–Φ–±–Α.
–ü–Μ–Ψ―â–Α–¥―¨
―Ä–Ψ–Φ–±–Α ―Ä–Α–≤–Ϋ–Α S=ah, –≥–¥–Β a - ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Ψ–Φ–±–Α, h - –≤―΄―¹–Ψ―²–Α ―Ä–Ψ–Φ–±–Α.
AD=AH+HD=21+54=75.
AD=AB=BC=CD (–Ω–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é ―Ä–Ψ–Φ–±–Α).
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABH.
ABH -
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι (―².–Κ. BH -
–≤―΄―¹–Ψ―²–Α), ―²–Ψ–≥–¥–Α –Ω–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
AB2=BH2+AH2
752=BH2+212
5625=BH2+441
BH2=5184
BH=72
S―Ä–Ψ–Φ–±–Α=AD*BH=75*72=5400
–û―²–≤–Β―²: S―Ä–Ψ–Φ–±–Α=5400
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ü–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 968√
–ü–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 968√
–Θ–Κ–Α–Ε–Η―²–Β –Ϋ–Ψ–Φ–Β―Ä–Α –≤–Β―Ä–Ϋ―΄―Ö ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Ι.
1) –£ ―²―É–Ω–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –≤―¹–Β ―É–≥–Μ―΄ ―²―É–Ω―΄–Β.
2) –£ –Μ―é–±–Ψ–Φ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η ―²–Ψ―΅–Κ–Ψ–Ι –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –¥–Β–Μ―è―²―¹―è –Ω–Ψ–Ω–Ψ–Μ–Α–Φ.
3) –Δ–Ψ―΅–Κ–Α, –Μ–Β–Ε–Α―â–Α―è –Ϋ–Α ―¹–Β―Ä–Β–¥–Η–Ϋ–Ϋ–Ψ–Φ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β –Κ –Ψ―²―Ä–Β–Ζ–Κ―É, ―Ä–Α–≤–Ϋ–Ψ―É–¥–Α–Μ–Β–Ϋ–Α –Ψ―² –Κ–Ψ–Ϋ―Ü–Ψ–≤ ―ç―²–Ψ–≥–Ψ –Ψ―²―Ä–Β–Ζ–Κ–Α.
 –û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ–Ψ–Μ–Ψ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –≤ –Κ–Ψ―²–Ψ―Ä–Ψ–Φ AB=BC –Η ∠ABC=25¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BOC. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ–Ψ–Μ–Ψ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –≤ –Κ–Ψ―²–Ψ―Ä–Ψ–Φ AB=BC –Η ∠ABC=25¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BOC. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α AL, ―É–≥–Ψ–Μ ALC ―Ä–Α–≤–Β–Ϋ 169¬Α, ―É–≥–Ψ–Μ ABC ―Ä–Α–≤–Β–Ϋ 160¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ACB. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α AL, ―É–≥–Ψ–Μ ALC ―Ä–Α–≤–Β–Ϋ 169¬Α, ―É–≥–Ψ–Μ ABC ―Ä–Α–≤–Β–Ϋ 160¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ACB. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
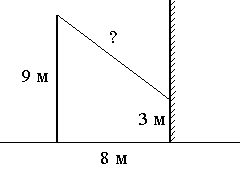 –û―² ―¹―²–Ψ–Μ–±–Α –≤―΄―¹–Ψ―²–Ψ–Ι 9 –Φ –Κ –¥–Ψ–Φ―É –Ϋ–Α―²―è–Ϋ―É―² –Ω―Ä–Ψ–≤–Ψ–¥, –Κ–Ψ―²–Ψ―Ä―΄–Ι –Κ―Ä–Β–Ω–Η―²―¹―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β 3 –Φ –Ψ―² –Ζ–Β–Φ–Μ–Η (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² –¥–Ψ–Φ–Α –¥–Ψ ―¹―²–Ψ–Μ–±–Α 8 –Φ. –£―΄―΅–Η―¹–Μ–Η―²–Β –¥–Μ–Η–Ϋ―É –Ω―Ä–Ψ–≤–Ψ–¥–Α.
–û―² ―¹―²–Ψ–Μ–±–Α –≤―΄―¹–Ψ―²–Ψ–Ι 9 –Φ –Κ –¥–Ψ–Φ―É –Ϋ–Α―²―è–Ϋ―É―² –Ω―Ä–Ψ–≤–Ψ–¥, –Κ–Ψ―²–Ψ―Ä―΄–Ι –Κ―Ä–Β–Ω–Η―²―¹―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β 3 –Φ –Ψ―² –Ζ–Β–Φ–Μ–Η (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² –¥–Ψ–Φ–Α –¥–Ψ ―¹―²–Ψ–Μ–±–Α 8 –Φ. –£―΄―΅–Η―¹–Μ–Η―²–Β –¥–Μ–Η–Ϋ―É –Ω―Ä–Ψ–≤–Ψ–¥–Α.

–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: