
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ510 –Є–Ј 1087 |
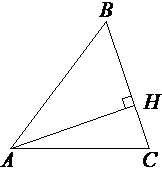 –Т –Њ—Б—В—А–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –≤—Л—Б–Њ—В–∞ AH —А–∞–≤–љ–∞ 20√
–Т –Њ—Б—В—А–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –≤—Л—Б–Њ—В–∞ AH —А–∞–≤–љ–∞ 20√
–Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABH
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є, —В.–Ї. AH -
–≤—Л—Б–Њ—В–∞.
–Ґ–Њ–≥–і–∞ –њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
AB2=AH2+BH2
402=(20√
1600=400*3+BH2
400=BH2
BH=20
–Я–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О:
cos∠B=BH/AB=20/40=1/2=0,5
–Ю—В–≤–µ—В: cos∠B=0,5
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
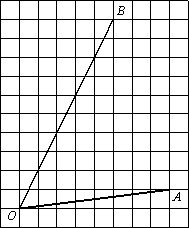 –Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ AOB.
–Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ AOB.
 –Ъ–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O –≤ —В–Њ—З–Ї–∞—Е A –Є B –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –њ–Њ–і —Г–≥–ї–Њ–Љ 82¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABO. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ъ–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O –≤ —В–Њ—З–Ї–∞—Е A –Є B –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –њ–Њ–і —Г–≥–ї–Њ–Љ 82¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABO. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, BC=8, sinA=0,4. –Э–∞–є–і–Є—В–µ AB.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, BC=8, sinA=0,4. –Э–∞–є–і–Є—В–µ AB.
 –Т –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –њ—А–Њ–≤–µ–і–µ–љ—Л –і–Є–∞–Љ–µ—В—А—Л
AD –Є BC, —Г–≥–Њ–ї OAB —А–∞–≤–µ–љ 70¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OCD.
–Т –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –њ—А–Њ–≤–µ–і–µ–љ—Л –і–Є–∞–Љ–µ—В—А—Л
AD –Є BC, —Г–≥–Њ–ї OAB —А–∞–≤–µ–љ 70¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OCD.
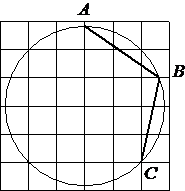 –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABC . –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABC . –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2021-12-15 15:59:07) —Е—Г–µ—Б–Њ—Б: )))