Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
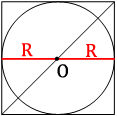Проведем радиусы окружности, как показано на рисунке.
Очевидно, что радиус вписанной окружности равен половине стороны квадрата, т.е.:
a=2R=2*4√2=8√2
По свойству квадрата, все углы прямые.
Следовательно, треугольник, образованный двумя сторонами и диагональю (обозначим ее как b) - прямоугольный.
Тогда можем применить теорему Пифагора:
b2=a2+a2
b2=2a2
b2=2(8√2)2
b2=2*64*2=256
b=√256=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
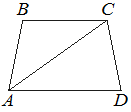Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
Площадь прямоугольного треугольника равна 200√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: