Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
AB=BC=CD=AD=DH+CH=24+2=26 (по
определению ромба).
Рассмотрим треугольник AHD.
AHD -
прямоугольный (т.к. AH -
высота), тогда по
теореме Пифагора:
AD2=AH2+DH2
262=AH2+242
676=AH2+576
AH2=676-576=100
AH=√100=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.
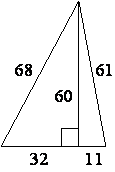Найдите площадь треугольника, изображённого на рисунке.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=16.
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
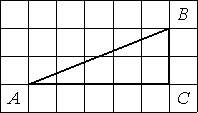Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: