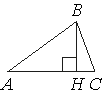В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
Рассмотрим треугольник ABH.
Это
прямоугольный треугольник, так как BH -
высота.
Тогда, по теореме о сумме углов треугольника:
180°=∠ABH+∠AHB+∠BAH
∠BAH=∠BAC=37° (так как это один и тот же угол).
180°=∠ABH+90°+37°
180°-90°-37°=∠ABH
∠ABH=53°
Ответ: 53
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD AB=CD, ∠BDA=54° и ∠BDC=33°. Найдите угол ABD. Ответ дайте в градусах.
В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: