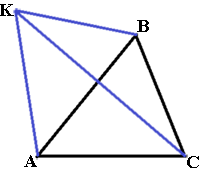
Стороны AC, AB, BC треугольника ABC равны 2√
По условию задачи ∠KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника). Сторона AC равная 2√
По условию задачи треугольник KAC подобен исходному треугольнику ABC. А значит углы этих треугольников соответственно равны (по определению подобных треугольников). Поэтому наибольшие углы двух рассматриваемых треугольников равны, т.е. ∠KAC=∠ABC. ∠ACK не равен ∠ACB ( т.к. KC пересекает сторону AB в точке, отличной от B), поэтому ∠ACK = ∠BAC. Следовательно, ∠AKC=∠ACB => cos(∠AKC)=cos(∠ACB).
Применяя теорему косинусов мы можем записать AB2=AC2+BC2-2*AC*BC*cos(∠ACB).
(√
5=4*2+1-4*√
5-9=-4*√
4=4*√
cos(∠ACB)=1/√
Для удобства домножим числитель и знаменатель на √
cos(∠ACB)=√
cos(∠AKC)=cos(∠ACB)=√
Ответ: √
Поделитесь решением
Присоединяйтесь к нам...
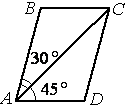Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-03-25 19:37:07) Администратор: Евгения, я добавил в решение пару строк, чтобы стало понятней.
(2017-03-25 12:34:31) Евгения: Добрый день, как в знаменателе в ответе появилась 2? Спасибо