ОГЭ, Математика. Геометрия: Задача №B93381 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Геометрия: Задача №B93381

Задача №727 из 1087
Условие задачи:

В треугольнике ABC с тупым углом ACB проведены высоты AA₁ и BB₁. Докажите, что треугольники A₁CB₁ и ACB подобны.

Решение задачи:

Рассмотрим треугольники AA₁C и BB₁C.
∠ACA₁=∠BCB₁, так как они вертикальные.
∠AA₁C=∠BB₁C, так как они прямые по условию задачи.
Следовательно, по первому признаку подобия треугольников, данные треугольники подобны.
Тогда, по определению подобных треугольников:
AC/BC=A₁C/B₁C
Преобразуем это равенство:
AC/A₁C=BC/B₁C
Рассмотрим треугольники A₁CB₁ и ABC.
∠ACB=∠A₁CB₁, так как они вертикальные.
Тогда, по второму признаку подобия, данные треугольники подобны.

ч.т.д.

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №3A541C

Площадь прямоугольного треугольника равна 32√3/3. Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.

Задача №225CE3

В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.

Задача №9915AE

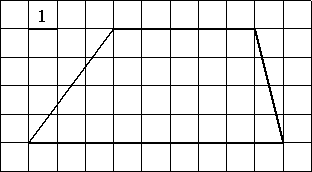Найдите площадь трапеции, изображённой на рисунке.

Задача №19F9D1

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника ABC.

Задача №F6FBB5

Синус острого угла A треугольника ABC равен 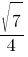. Найдите CosA.

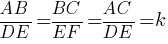
Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X Подобные треугольники
— треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.

k - называется коэффициент подобия.

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.