Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
По
теореме об описанной окружности, центр описанной окружности лежит на точке пересечения
серединных перпендикуляров сторон треугольника.
У
прямоугольного треугольника центр окрудности лежит на середине гипотенузы, так же как и в треугольнике нашей задачи, следовательно данный треугольник
прямоугольный.
Следовательно, можно применить
теорему Пифагора:
AB2=BC2+AC2
AB - диаметр окружности, так как проходит через центр.
Тогда AB=2*R=2*15=30.
302=BC2+242
900=BC2+576
BC2=900-576=324
BC=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
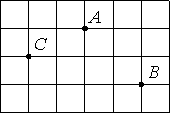На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
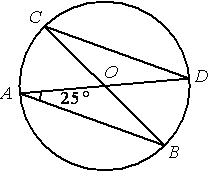В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
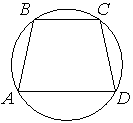Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: