
 Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
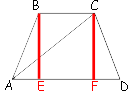 Обозначим ключевые точки, как показано на рисунке и проведем
высоты BE и CF.
Обозначим ключевые точки, как показано на рисунке и проведем
высоты BE и CF.
Рассмотрим четырехугольник BCFE.
∠CFE=∠BEF=90° (так как BE и CF -
высоты).
∠CBE=180°-∠BEF=180°-90°=90° (так как это
внутренние односторонние углы при параллельных прямых AD и BC и секущей BE).
∠BCF=90° (аналогично углу CBE).
Получается, что BCFE -
прямоугольник.
Тогда BE=CF и BC=EF=16 (по
свойству прямоугольника).
Рассмотрим треугольники ABE и CDF.
AB=CD=58 (так как
трапеция равнобедренная).
BE=CF (это мы выяснили ранее).
∠ABC=∠DCB (так как по
свойству равнобедренной трапеции, угли при одном основании равны).
Следовательно, равно и следующее равенство:
∠ABC-90°=∠DCB-90° - это и есть углы ABE и DCF соответственно, т.е.:
∠ABE=∠DCF
Тогда, по
второму признаку равенства треугольников, данные треугольники равны.
Следовательно, AE=FD.
AD=AE+EF+FD=AE+BC+AE=2AE+16=96
2AE=80
AE=40=FD
Найдем
высоту CF по
теореме Пифагора:
CD2=CF2+FD2
582+CF2+402
3364=CF2+1600
CF2=1764
CF=42
Найдем AC по
теореме Пифагора:
AC2=CF2+AF2
AC2=CF2+(AE+EF)2
AC2=422+(40+16)2
AC2=1764+3136=4900
AC=70
Ответ: 70
Поделитесь решением
Присоединяйтесь к нам...
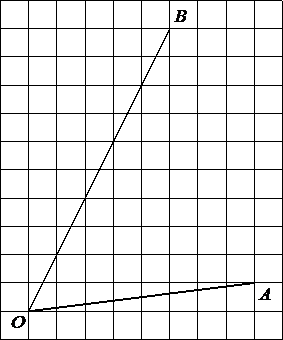 Найдите тангенс угла
AOB.
Найдите тангенс угла
AOB.
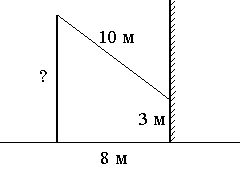 От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
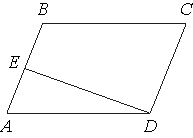 Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
 Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
 Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.

Комментарии: