
 К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
 Проведем отрезок ОВ.
Проведем отрезок ОВ.
Отрезок OB - это радиус окружности и этот отрезок перпендикулярен AB (по
свойству
касательной).
Следовательно, треугольник AOB -
прямоугольный, тогда, по
теореме Пифагора:
AO2=AB2+OB2
852=402+OB2
7225=1600+OB2
OB2=5625
OB=75=R
Ответ: 75
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 3√
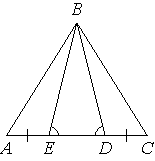 На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
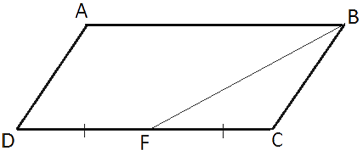 Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
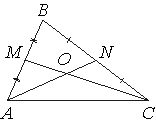 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=18, CM=21. Найдите OM.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=18, CM=21. Найдите OM.
Стороны AC, AB, BC треугольника ABC равны 2√

Комментарии:
(2019-05-05 11:40:38) Администратор: Коля, Вы имеете ввиду написать само слово \"Дано\"?
(2019-05-05 10:35:58) коля : напишите пожалуста дано спасибо