В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
По условию задачи треугольник ABC -
равнобедренный.
BM является не только
медианой, но и
высотой (по
третьему свойству равнобедренного треугольника).
Следовательно:
1) AM=MC=AC/2=56/2=28
2) Треугольник ABM
прямоугольный.
Тогда, по
теореме Пифагора:
AB2=BM2+AM2
532=BM2+282
2809=BM2+784
BM2=2025
BM=45
Ответ: 45
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=60°. Найдите угол NMB. Ответ дайте в градусах.
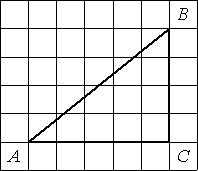Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
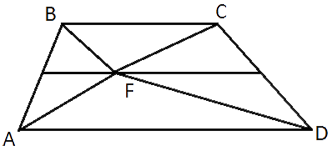На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: