Площадь прямоугольного треугольника равна 512√
Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin30°=1/2 (
табличное значение)
sin30°=a/c=1/2 (по
определению синуса)
c=2a
По
теореме Пифагора:
a2+b2=c2
a2+b2=(2a)2
b2=3a2
b=a√
Из условия: Sтреугольника=ab/2=512√
a*a√
Сокращаем √
a2=512*2=1024
a=32
Ответ: a=32
Поделитесь решением
Присоединяйтесь к нам...
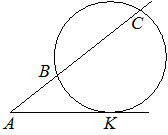Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: