Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Радиус вписанной окружности можно вычислить по формуле R=(AC+CB-AB)/2. Для этого необходимо вычислить длины всех сторон данного треугольника.
Рассмотрим треугольник ABC.
По
определению tgBAC=CB/AC=4/3 => AC=3*CB/4.
По
теореме Пифагора AB2=AC2+CB2
AB2=(3*CB/4)2+CB2
AB2=9*CB2/16+CB2
AB2=25*CB2/16
AB=5*CB/4
Необходимо вычислить CB.
По
теореме о сумме углов треугольника для треугольника ABC:
/ABC=180°-90°-/BAC
Для треугольника BCP:
/ABC=180°-90°-/BCP
Следовательно, /BAC=/BCP.
Рассмотрим треугольник BCP.
По
определению tgBCP=BP/CP=4/3 => CP=3*BP/4.
По
теореме Пифагора CB2=CP2+BP2
CB2=(3*BP/4)2+BP2
CB2=9*BP2/19+BP2
CB2=25*BP2/16
CB=5*BP/4
BP=4*CB/5
r=(BP+CP-CB)/2
2*r=BP+3*BP/4-CB
2*8=7*BP/4-CB
16=7*(4*CB/5)/4-CB
16=(7*4)*CB/(5*4)-CB
16=7*CB/5-CB
16=2*CB/5 |:2
8=CB/5
CB=8*5=40
Вычислив CB, мы можем вычислить AB и AC, указанные выше:
AB=5*CB/4=5*40/4=5*10=50
AC=3*CB/4=3*40/4=3*10=30
R=(AC+CB-AB)/2, тогда получаем:
R=(30+40-50)/2=20/2=10
Ответ: R=10.
Поделитесь решением
Присоединяйтесь к нам...
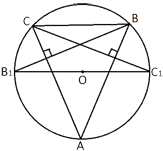Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-02-02 18:44:10) Марина: Первый способ решения приводит к верному ответу, хотя используется теорема синусов. Как известно теорема синусов связывает зависимостью стороны, синусы и радиус ОПИСАННОЙ окружности треугольника, что и видно в решении (2R=AB). А нам нужен радиус вписанной окружности.
(2015-02-01 14:19:29) Администратор: Марина, да, Вы правы, изучу как это получилось...
(2015-02-01 11:51:37) Марина: Первый способ решения приводит к верному ответу, хотя используется теорема синусов. Как известно теорема синусов связывает зависимостью стороны, синусы и радиус ОПИСАННОЙ окружности треугольника, что и видно в решении (2R=AB). А нам нужен радиус вписанной окружности.