В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
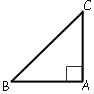SABC=AB*AC/2
Пусть угол, равный 45° будет угол В.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=90°+45°+∠C
∠C=45°
Следовательно, по
свойству равнобедренного треугольника, треугольник ABC -
равнобедренный.
Значит AB=AC.
По
теореме Пифагора:
BC2=AB2+AC2
BC2=AB2+AB2
822=2AB2
6724=2AB2
AB2=3362
SABC=AB*AC/2
SABC=AB2/2=3362/2=1681
Ответ: SABC=1681
Поделитесь решением
Присоединяйтесь к нам...
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 55°. Найдите величину угла OAB.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
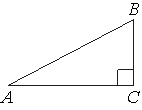В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 21°?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: