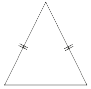
Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
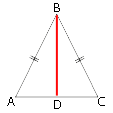Проведем высоту BD.
По
свойству
равнобедренного треугольника:
высота, проведенная к основанию так же является и
медианой.
Следовательно, AD=DC=AC/2=30/2=15
Чтобы вычислить эту высоту треугольника воспользуемся
теоремой Пифагора:
AB2=BD2+AD2
252=BD2+152
625=BD2+225
BD2=400
BD=20
Площадь треугольника: S=ah/2=AC*BD/2
S=30*20/2=300
Ответ: S=300
Поделитесь решением
Присоединяйтесь к нам...
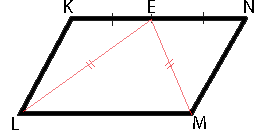В параллелограмме KLMN точка E — середина стороны KN. Известно, что EL=EM. Докажите, что данный параллелограмм — прямоугольник.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
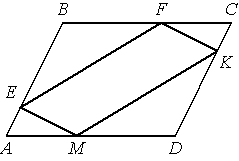В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD.
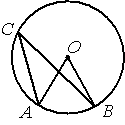Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: