Катеты прямоугольного треугольника равны √
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=12+(√
AB2=1+15=16
AB=4
Меньший угол лежит напротив меньшей стороны, 1<√
Ответ: 0,25
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
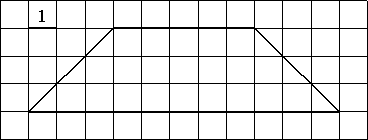Найдите площадь трапеции, изображённой на рисунке.
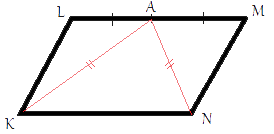В параллелограмме KLMN точка E — середина стороны KN. Известно, что EL=EM. Докажите, что данный параллелограмм — прямоугольник.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-03-12 18:49:47) Администратор: Дима, если AB2=16, то AB=√
(2015-03-12 15:44:47) Дима: 4 откуда ?