Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7.5, а AB=2.
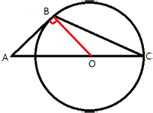Отрезок AC равен сумме отрезков AO и OC, OC - равен радиусу окружности, т.е. 7,5/2=3,75. Найдем AO.
Проведем отрезок BO. BO - так же является радиусом окружности. AB -
касательная к окружности, следовательно AB перпендикулярен BO (по
свойству касательной).
Значит треугольник ABO -
прямоугольный, тогда по
теореме Пифагора:
AO2=AB2+BO2
AO2=22+3,752
AO2=4+14,0625=18,0625
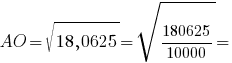
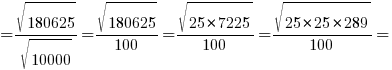
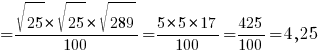
AC=AO+OC=4,25+3,75=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь трапеции, изображённой на рисунке.
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=40.
Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
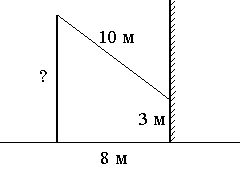От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-02-07 23:55:24) Администратор: Марина, я немного расписал решение...
(2018-02-07 16:48:46) марина: как взять корень из этого числа