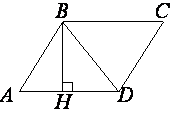Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
Площадь
параллелограмма равна произведению высоты на сторону параллелограмма. Sпараллелограмма=BH*AD
Найдем высоту. По
теореме Пифагора запишем:
BD2=HD2+BH2
852=752+BH2
7225=5625+BH2
BH2=1600
BH=40
Sпараллелограмма=BH*AD=BH*(AH+HD)=40*(6+75)=40*81=3240
Ответ: Sпараллелограмма=3240
Поделитесь решением
Присоединяйтесь к нам...
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K,
длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Найдите площадь треугольника, изображённого на рисунке.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: