Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 5 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Радиус вписанной окружности можно вычислить по формуле R=(AC+CB-AB)/2. Для этого необходимо вычислить длины всех сторон данного треугольника.
Рассмотрим треугольник ABC.
По
определению tgABC=AC/CB=2,4 => AC=2,4*CB.
По
теореме Пифагора AB2=AC2+CB2
AB2=(2,4*CB)2+CB2
AB2=(CB/2,4)2+(2,4*CB/2,4)2
AB2=5,76*CB2+CB2
AB2=6,76*CB2
AB=2,6*CB
Необходимо вычислить CB.
Рассмотрим треугольник BCP.
По
определению tgABC=CP/BP=2,4 => CP=2,4*BP
По
теореме Пифагора CB2=CP2+BP2
CB2=(2,4*BP)2+BP2
CB2=6,76*BP2
CB=2,6*BP
BP=CB/2,6
r=(BP+CP-CB)/2
2*r=BP+2,4*BP-2,6*BP
2*5=0,8*BP
BP=12,5
CB=2,6*BP=2,6*12,5=32,5
Вычислив CB, мы можем вычислить AB и AC, указанные выше:
AB=2,6*CB=2,6*32,5=84,5
AC=2,4*CB=2,4*32,5=78
R=(AC+CB-AB)/2, тогда получаем:
R=(78+32,5-84,5)/2=13.
Ответ: R=13.
Поделитесь решением
Присоединяйтесь к нам...
Косинус острого угла A треугольника ABC равен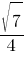 
. Найдите sinA.
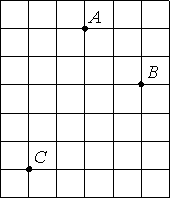На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
Человек, рост которого равен 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина тени человека равна 2 м. Определите высоту фонаря (в метрах).
Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: