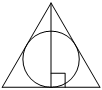
Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
Из
четвертого свойства равностороннего треугольника найдем его сторону:
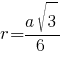
6r=a√3
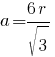
По второму свойству равностороннего треугольника:
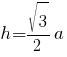
Подставляем значение "a":
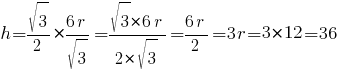
Ответ: 36
Поделитесь решением
Присоединяйтесь к нам...
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
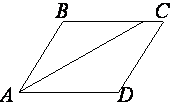Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 80°. Найдите величину угла OCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
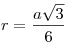
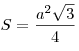
Комментарии: