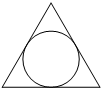
Радиус окружности, вписанной в равносторонний треугольник, равен 2√
По
свойству равностороннего треугольника:
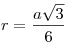
Тогда:
6r=a√
a=6r/√
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=38°. Найдите угол NMB. Ответ дайте в градусах.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: