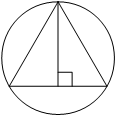
Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
По
третьему свойству
равностороннего треугольника:
R=a√
6=a√
18=a√
a=18/√
По второму свойству:
h=a*√
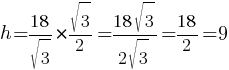
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
У треугольника со сторонами 4 и 16 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 4. Чему равна высота, проведённая ко второй стороне?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 2 м, высота фонаря 4 м?
Центральный угол AOB равен
60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 7.
Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: