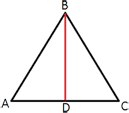
Сторона равностороннего треугольника равна 10√
По
определению равностороннего треугольника:
AB=BC=AC=10√
По
свойству равностороннего треугольника,
биссектриса является так же и
медианой, и
высотой.
Следовательно:
1) BD перпендикулярен AC (т.к. BD -
высота), т.е. треугольник ABD -
прямоугольный.
2) AD=AC/2.
По
теореме Пифагора:
AB2=BD2+AD2
AB2=BD2+(AC/2)2
(10√
100*3=BD2+(5√
300=BD2+25*3
300=BD2+75
BD2=225
BD=15
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
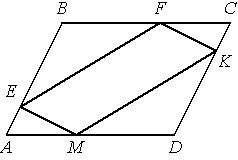В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 4, тангенс угла BAC равен 0,75. Найдите радиус вписанной окружности треугольника ABC.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-03-30 23:06:34) Администратор: Акиф, в решении есть ссылки на материалы, на которые я ссылаюсь в решении - это первое. Поясните, начиная с какой строки Вам непонятно...Я обязательно поясню.
(2017-03-29 22:54:04) Акиф: Можете по подробней объяснить ?