
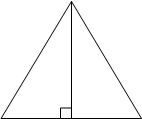
 Высота равностороннего треугольника равна
15√
Высота равностороннего треугольника равна
15√
Обозначим сторону
равностороннего треугольника как a.
Высота является
медианой (по
свойству равностороннего треугольника), следовательно, высота делит сторону треугольника пополам.
Тогда, по
теореме Пифагора можем записать:
a2=(a/2)2+(15√
a2-(a/2)2=152*3
a2-a2/4=225*3
3a2/4=675
3a2=2700
a2=900
a=30
Так как все стороны равны, то периметр P=3*а=90
Ответ: P=90.
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
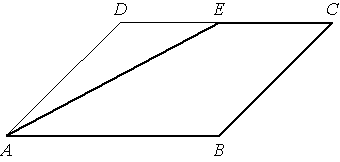 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
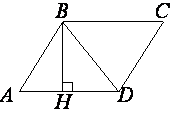 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
 Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Комментарии:
(2015-11-10 17:58:16) Администратор: Ирина, a2-a2/4=4a2/4-a2/4=(4a2-a2)/4=3a2/4, т.е. просто привели к общему знаменателю.
(2015-11-08 15:42:26) : Большое спасибо
(2015-11-08 15:15:50) Администратор: Ирина, a2-a2/4=4a2/4-a2/4=(4a2-a2)/4=3a2/4, т.е. просто привели к общему знаменателю.
(2015-11-08 15:09:28) Ирина: Скажите пожалуйста, откуда в четвертом действии 3a?