Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
Периметр
параллелограмма:
P=AB+BC+CD+AD
AB=CD и BC=AD (по
свойству параллелограмма)
P=AB+BC+AB+BC=2(AB+BC)
∠DAK=∠AKB (т.к. это
накрест-лежащие углы).
Следовательно ∠AKB=∠KAB (т.к. AK -
биссектриса)
Получается, что треугольник ABK -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BK=5
P=2(AB+BC)=2(AB+BK+CK)=2(5+5+14)=2*24=48
Ответ: 48
Поделитесь решением
Присоединяйтесь к нам...
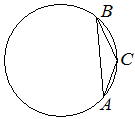В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
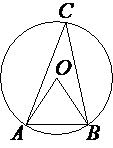Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 320 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: