В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
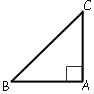SABC=AB*AC/2
Пусть угол, равный 45° будет угол В.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=90°+45°+∠C
∠C=45°
Следовательно, по
свойству равнобедренного треугольника, треугольник ABC -
равнобедренный.
Значит AB=AC.
По
теореме Пифагора:
BC2=AB2+AC2
BC2=AB2+AB2
822=2AB2
6724=2AB2
AB2=3362
SABC=AB*AC/2
SABC=AB2/2=3362/2=1681
Ответ: SABC=1681
Поделитесь решением
Присоединяйтесь к нам...
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Найдите угол ABC. Ответ дайте в градусах.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=84 и BC=BM. Найдите AH.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: