
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ600 –Η–Ζ 1087 |
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α BE –Η –Φ–Β–¥–Η–Α–Ϋ–Α AD –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ―΄ –Η –Η–Φ–Β―é―² –Ψ–¥–Η–Ϋ–Α–Κ–Ψ–≤―É―é –¥–Μ–Η–Ϋ―É, ―Ä–Α–≤–Ϋ―É―é 28. –ù–Α–Ι–¥–Η―²–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α BE –Η –Φ–Β–¥–Η–Α–Ϋ–Α AD –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ―΄ –Η –Η–Φ–Β―é―² –Ψ–¥–Η–Ϋ–Α–Κ–Ψ–≤―É―é –¥–Μ–Η–Ϋ―É, ―Ä–Α–≤–Ϋ―É―é 28. –ù–Α–Ι–¥–Η―²–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABD.
BO –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ AD (–Ω–Ψ ―É―¹–Μ–Ψ–≤–Η―é –Ζ–Α–¥–Α―΅–Η), ―².–Β. ∠BOD=∠BOA=90¬Α.
∠ABO=∠DBO (―².–Κ. BE -
–±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α).
–ü–Ψ–Μ―É―΅–Α–Β―²―¹―è, ―΅―²–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ABO –Η DBO ―Ä–Α–≤–Ϋ―΄ (–Ω–Ψ
–≤―²–Ψ―Ä–Ψ–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É ―Ä–Α–≤–Β–Ϋ―¹―²–≤–Α ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤).
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, AB=BD.
–Δ.–Β. ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABD -
―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―΄–Ι.
BO -
–±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ –Η
–Φ–Β–¥–Η–Α–Ϋ–Α, –Η
–≤―΄―¹–Ψ―²–Α (–Ω–Ψ ―²―Ä–Β―²―¨–Β–Φ―É
―¹–≤–Ψ–Ι―¹―²–≤―É ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α).
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, AO=OD=AD/2=28/2=14.
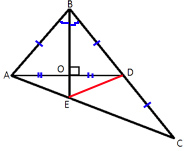 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ ED –Η ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ BEC.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ ED –Η ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ BEC.
ED -
–Φ–Β–¥–Η–Α–Ϋ–Α ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, ―²–Α–Κ –Κ–Α–Κ –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É BC –Ω–Ψ–Ω–Ψ–Μ–Α–Φ.
–ü–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ EDC –Η EDB ―Ä–Α–≤–Ϋ―΄ (–Ω–Ψ –≤―²–Ψ―Ä–Ψ–Φ―É
―¹–≤–Ψ–Ι―¹―²–≤―É –Φ–Β–¥–Η–Α–Ϋ―΄). SEDC=SEDB=(BE*OD)/2=(28*14)/2=14*14=196
SABE=(BE*AO)/2=(28*14)/2=196
–Δ.–Β.
SABE=SEDC=SEDB=196
–Δ–Ψ–≥–¥–Α, SAB–Γ=3*196=588
AD -
–Φ–Β–¥–Η–Α–Ϋ–Α ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC (–Ω–Ψ ―É―¹–Μ–Ψ–≤–Η―é), ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ –¥–Β–Μ–Η―² ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –Ϋ–Α –¥–≤–Α ―Ä–Α–≤–Ϋ―΄―Ö –Ω–Ψ –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABD –Η ACD (–Ω–Ψ
–≤―²–Ψ―Ä–Ψ–Φ―É ―¹–≤–Ψ–Ι―¹―²–≤―É –Φ–Β–¥–Η–Α–Ϋ―΄).
SABD=(AD*BO)/2=SABC/2
(28*BO)/2=588/2
BO=588/28=21
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABO, –Ψ–Ϋ
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι, ―²–Ψ–≥–¥–Α –Ω―Ä–Η–Φ–Β–Ϋ–Η–Φ
―²–Β–Ψ―Ä–Β–Φ―É –ü–Η―³–Α–≥–Ψ―Ä–Α:
AB2=BO2+AO2
AB2=212+142
AB2=441+196=637
AB=√
BC=2AB=2*7√
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ AOE.
OE=BE-BO=28-21=7
–Δ–Α–Κ –Κ–Α–Κ ―ç―²–Ψ―² ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―²–Ψ–Ε–Β
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι, ―²–Ψ –Φ–Ψ–Ε–Ϋ–Ψ –Ω―Ä–Η–Φ–Β–Ϋ–Η―²―¨
―²–Β–Ψ―Ä–Β–Φ―É –ü–Η―³–Α–≥–Ψ―Ä–Α:
AE2=AO2+OE2
AE2=142+72=196+49=245
AE=√
–Δ–Α–Κ –Κ–Α–Κ BE -
–±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α, ―²–Ψ –Η―¹–Ω–Ψ–Μ―¨–Ζ―É―è –Β–Β
–Ω–Β―Ä–≤–Ψ–Β ―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Ζ–Α–Ω–Η―à–Β–Φ:
BC/AB=CE/AE
14√
2=CE/(7√
CE=14√
AC=AE+CE=7√
–û―²–≤–Β―²: AB=7√
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ö–Α―Ä―²–Η–Ϋ–Κ–Α –Η–Φ–Β–Β―² ―³–Ψ―Ä–Φ―É –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 24 ―¹–Φ –Η 37 ―¹–Φ. –ï―ë –Ϋ–Α–Κ–Μ–Β–Η–Μ–Η –Ϋ–Α –±–Β–Μ―É―é –±―É–Φ–Α–≥―É ―²–Α–Κ, ―΅―²–Ψ –≤–Ψ–Κ―Ä―É–≥ –Κ–Α―Ä―²–Η–Ϋ–Κ–Η –Ω–Ψ–Μ―É―΅–Η–Μ–Α―¹―¨ –±–Β–Μ–Α―è –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Α –Ψ–¥–Η–Ϋ–Α–Κ–Ψ–≤–Ψ–Ι ―à–Η―Ä–Η–Ϋ―΄. –ü–Μ–Ψ―â–Α–¥―¨, –Κ–Ψ―²–Ψ―Ä―É―é –Ζ–Α–Ϋ–Η–Φ–Α–Β―² –Κ–Α―Ä―²–Η–Ϋ–Κ–Α ―¹ –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Ψ–Ι, ―Ä–Α–≤–Ϋ–Α 1440 ―¹–Φ2. –ö–Α–Κ–Ψ–≤–Α ―à–Η―Ä–Η–Ϋ–Α –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Η? –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö.
–ö–Α―Ä―²–Η–Ϋ–Κ–Α –Η–Φ–Β–Β―² ―³–Ψ―Ä–Φ―É –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 24 ―¹–Φ –Η 37 ―¹–Φ. –ï―ë –Ϋ–Α–Κ–Μ–Β–Η–Μ–Η –Ϋ–Α –±–Β–Μ―É―é –±―É–Φ–Α–≥―É ―²–Α–Κ, ―΅―²–Ψ –≤–Ψ–Κ―Ä―É–≥ –Κ–Α―Ä―²–Η–Ϋ–Κ–Η –Ω–Ψ–Μ―É―΅–Η–Μ–Α―¹―¨ –±–Β–Μ–Α―è –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Α –Ψ–¥–Η–Ϋ–Α–Κ–Ψ–≤–Ψ–Ι ―à–Η―Ä–Η–Ϋ―΄. –ü–Μ–Ψ―â–Α–¥―¨, –Κ–Ψ―²–Ψ―Ä―É―é –Ζ–Α–Ϋ–Η–Φ–Α–Β―² –Κ–Α―Ä―²–Η–Ϋ–Κ–Α ―¹ –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Ψ–Ι, ―Ä–Α–≤–Ϋ–Α 1440 ―¹–Φ2. –ö–Α–Κ–Ψ–≤–Α ―à–Η―Ä–Η–Ϋ–Α –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Η? –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö.
–ß–Β―Ä–Β–Ζ ―¹–Β―Ä–Β–¥–Η–Ϋ―É K –Φ–Β–¥–Η–Α–Ϋ―΄ BM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Η –≤–Β―Ä―à–Η–Ϋ―É A –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –Ω―Ä―è–Φ–Α―è, –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―â–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ―É BC –≤ ―²–Ψ―΅–Κ–Β P. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α BKP –Κ –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α AMK.
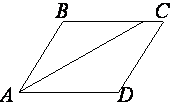 –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É –Ψ―¹―²―Ä–Ψ–≥–Ψ ―É–≥–Μ–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD, –Β―¹–Μ–Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―É–≥–Μ–Α A –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι BC ―É–≥–Ψ–Μ, ―Ä–Α–≤–Ϋ―΄–Ι 14¬Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É –Ψ―¹―²―Ä–Ψ–≥–Ψ ―É–≥–Μ–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD, –Β―¹–Μ–Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―É–≥–Μ–Α A –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι BC ―É–≥–Ψ–Μ, ―Ä–Α–≤–Ϋ―΄–Ι 14¬Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
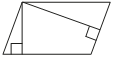 –ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Α 60, –Α –¥–≤–Β –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Α–≤–Ϋ―΄ 4 –Η 20. –ù–Α–Ι–¥–Η―²–Β –Β–≥–Ψ –≤―΄―¹–Ψ―²―΄. –£ –Ψ―²–≤–Β―²–Β ―É–Κ–Α–Ε–Η―²–Β –±–Ψ–Μ―¨―à―É―é –≤―΄―¹–Ψ―²―É.
–ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Α 60, –Α –¥–≤–Β –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Α–≤–Ϋ―΄ 4 –Η 20. –ù–Α–Ι–¥–Η―²–Β –Β–≥–Ψ –≤―΄―¹–Ψ―²―΄. –£ –Ψ―²–≤–Β―²–Β ―É–Κ–Α–Ε–Η―²–Β –±–Ψ–Μ―¨―à―É―é –≤―΄―¹–Ψ―²―É.
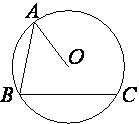 –Δ–Ψ―΅–Κ–Α O βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä–Ψ–Ι –Μ–Β–Ε–Α―² ―²–Ψ―΅–Κ–Η A, B –Η C. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ ∠ABC=43¬Α –Η ∠OAB=13¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ BCO. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–Δ–Ψ―΅–Κ–Α O βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä–Ψ–Ι –Μ–Β–Ε–Α―² ―²–Ψ―΅–Κ–Η A, B –Η C. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ ∠ABC=43¬Α –Η ∠OAB=13¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ BCO. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.

–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: