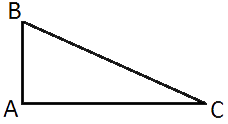
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
SABC=AB*AC/2
Пусть угол, равный 45° будет угол В.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=90°+45°+∠C
∠C=45°
Следовательно, по
свойству равнобедренного треугольника, треугольник ABC -
равнобедренный.
Значит AB=AC.
По
теореме Пифагора:
BC2=AB2+AC2
BC2=AB2+AB2
702=2AB2
4900=2AB2
AB2=2450
SABC=AB*AC/2
SABC=AB2/2=2450/2=1225
Ответ: SABC=1225
Поделитесь решением
Присоединяйтесь к нам...
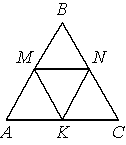В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
Площадь прямоугольного треугольника равна 2450√
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-02-11 01:22:37) Кристина: Найдите площадь прямоугольного треугольника, если его катет и гипоте- нуза равны соответственно 12 и 13.